<h3><a title="题目描述" href="https://leetcode-cn.com/problems/sqrtx">题目描述</a></h3>

<h4>0分的投机取巧歪曲题意解法:</h4>
<pre class="EnlighterJSRAW" data-enlighter-language="null">class Solution:
def mySqrt(self, x: int) -> int:
return (int(x ** 0.5))</pre>
<h4>二分法:</h4>
<pre class="EnlighterJSRAW" data-enlighter-language="null">class Solution:
def mySqrt(self, x: int) -> int:
if x == 0:
return 0
left = 1
right = x // 2
while left < right:
mid = (left + right + 1) // 2
square = mid * mid
if square > x:
right = mid - 1
else:
left = mid
return left</pre>
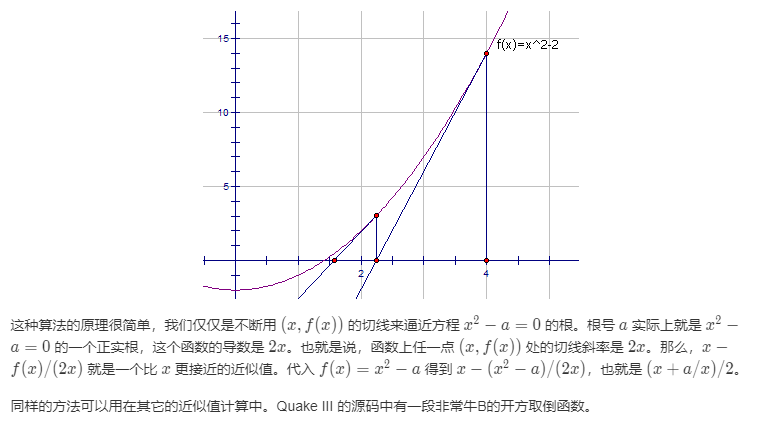
<h4>牛顿法:</h4>
<pre class="EnlighterJSRAW" data-enlighter-language="null">class Solution:
def mySqrt(self, x):
if x < 0:
raise Exception('不能输入负数')
if x == 0:
return 0
cur = 1
while True:
pre = cur
cur = (cur + x / cur) / 2
if abs(cur - pre) < 1e-6:
return int(cur)</pre>
#### Note:
下面这种方法可以很有效地求出根号 a 的近似值:首先随便猜一个近似值 x,然后不断令 x 等于 x 和 a/x 的平均数,迭代个六七次后 x 的值就已经相当精确了。
例如,我想求根号 2 等于多少。假如我猜测的结果为 4,虽然错的离谱,但你可以看到使用牛顿迭代法后这个值很快就趋近于根号 2 了:
> ( 4 + 2/ 4 ) / 2 = 2.25
> ( 2.25 + 2/ 2.25 ) / 2 = 1.56944..
> ( 1.56944..+ 2/1.56944..) / 2 = 1.42189..
> ( 1.42189..+ 2/1.42189..) / 2 = 1.41423..
Leetcode69 x的平方根
