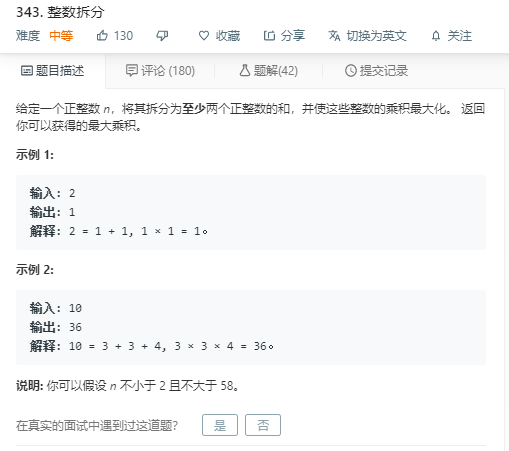
<h3><a title="题目描述" href="https://leetcode-cn.com/problems/integer-break">题目描述</a></h3>  <h4>我的解法(贪心)</h4> <pre class="EnlighterJSRAW" data-enlighter-language="python">class Solution: def integerBreak(self, n: int) -> int: dp = [0] * 60 dp[2],dp[3],dp[4] = 1,2,4 for i in range(5,59): x = i // 3 y = (i - 3*x) // 2 while(x*3+y*2 != i): x -= 1 y = (i - 3*x)// 2 dp[i] = 3**x * 2**y return dp[n] </pre> <p> </p> #### Note: ##### @解题思路： |n |拆分方式 |乘积 | | | ------------ | ------------ | ------------ | ------------ | |2 |1+1 |1 |不拆分，2>1\*1 | |3 |1+2 |2 |不拆分，3>1\*2 | |4 |2+2 |4 |拆分 | |5 |2+3 |6 |拆分 | |6 |3+3 |9 |拆分 | |7 |2+2+3 |12 |拆分 | 观察上述式子，有 - 结论1：大数字尽可能拆为小因子，通过指数增长获得更大的乘积 - **数字应尽可能拆成尽可能多3的和，但余数为1时 应该把最后1个3+1变为1+1**,这就是对我上面给的算法优化的方法。 - 我自己的方法一开始想到的是dp写着写着就变成贪心了 开了个数组 实际上没必要。 <h4>细节上更优的贪心解法</h4> <pre class="EnlighterJSRAW" data-enlighter-language="python">class Solution: def integerBreak(self, n: int) -> int: if n <= 3 : return n-1 a, b = n // 3, n % 3 if(b==0):return pow(3,a) if(b==1):return pow(3,a-1)*4 return pow(3,a)*2 </pre> <p> </p> <h4>动态规划法</h4> <pre class="EnlighterJSRAW" data-enlighter-language="python">class Solution: def integerBreak(self, n): dp = [1 for _ in range(n + 1)] dp[0] = 0 dp[1] = 1 dp[2] = 1 for i in range(3, n + 1): dp[i] = max(max(dp[i - 1], i - 1), 2 * max(dp[i - 2], i - 2), 3 * max(dp[i - 3], i - 3)) return dp[n] </pre> <p> </p> #### Note: ##### @解题思路： 动态规划好像都是一开始很难想。。。但是看又很容易看得懂。。。 初始的motivation这道题我也没想明白=。= 积攒经验吧。。。