## 降维主要方法
- 投影
- 流形学习
### 流形学习
> 用到的时候再看
### PCA
识别出最接近数据的超平面,然后将数据**投影**到上面。
#### 保留差异性
使原始数据集与投影之间的均方距离最小的超平面
#### 主成分
n维特征 映射 到 k维上,k维**正交**特征被称为主成分
PCA可以在训练集中识别哪个平面对差异性贡献度最高,所选出的超平面的数量与数据集维度的数量相同。
第$i$ 条轴的**单位向量**就叫第$i$个主成分(PC),下图中第一个主成分是$c_1$,第二个主成分是$c_2$
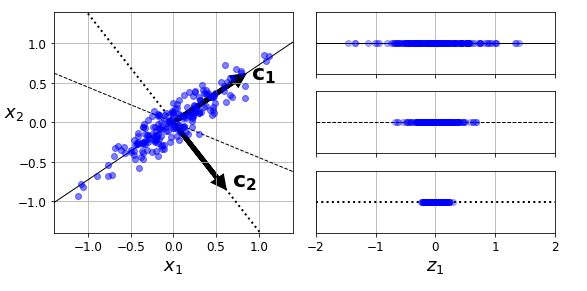
> 主成分的方向是不稳定的(即举例来说c1 c2可能反向,甚至旋转或者互换),但它们所定义的平面不变。
#### PCA - SVD
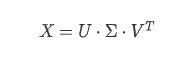
SVD将X分解为3个矩阵,$X$为训练集矩阵,$V^T$为主成分矩阵
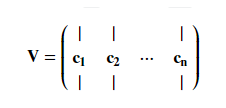
<pre class="EnlighterJSRAW" data-enlighter-language="null">X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
c1 = Vt.T[:, 0]
c2 = Vt.T[:, 1]
# np.allclose() 判断2个向量是不是每一元素都相近 误差1e-05范围</pre>
##### 低维度投影
一旦确定了主成分,**将数据集投影到前k个主成分所定义的超平面上**,这就是PCA**降维**的方法。
而要将数据集投影到超平面上只需简单计算训练集矩阵$X$与矩阵$W_k$的**点积**即可
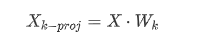
##### 解压缩还原 / 逆转换
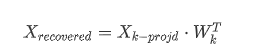
<pre class="EnlighterJSRAW" data-enlighter-language="null">W2 = Vt.T[:, :2]
X2D = X_centered.dot(W2) # X_centered为训练集
X2D_using_svd = X2D</pre>
#### PCA -Scikit-Learn
> 还是用SVD实现的,它会自动集中数据。
<pre class="EnlighterJSRAW" data-enlighter-language="null">from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
X2D = pca.fit_transform(X)
# 第一个主成分pca.components.T[:,0]</pre>
##### 方差解释率
表示每个主成分轴对整个数据集的方差的贡献度
<pre class="EnlighterJSRAW" data-enlighter-language="null">>>> pca.explained_variance_ratio_ # 通过explained_variance_ratio_访问
array([0.84248607, 0.14631839])</pre>
##### 选择所降维的维度k
计算保留训练集方差95%所需的最低维度d
<pre class="EnlighterJSRAW" data-enlighter-language="null">from sklearn.decomposition import PCA
pca = PCA()
pca.fit(X_train)
cumsum = np.cumsum(pca.explained_variance_ratio_)
d = np.argmax(cumsum >= 0.95) + 1
n_components = d</pre>
**推荐**用这种
<pre class="EnlighterJSRAW" data-enlighter-language="null">from sklearn.decomposition import PCA
pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X_train)</pre>
#### PCA压缩
<pre class="EnlighterJSRAW" data-enlighter-language="null">from six.moves import urllib
try:
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1)
mnist.target = mnist.target.astype(np.int64)
except ImportError:
from sklearn.datasets import fetch_mldata
mnist = fetch_mldata('MNIST original')
from sklearn.model_selection import train_test_split
X = mnist["data"]
y = mnist["target"]
#784个特征转为154个特征,压缩了数据集大小又保留了主要特征,提高分类器性能
X_train, X_test, y_train, y_test = train_test_split(X, y)
pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X_train)
X_recovered = pca.inverse_transform(X_reduced) #解压缩还原
# 绘制图像
def plot_digits(instances, images_per_row=5, **options):
size = 28
images_per_row = min(len(instances), images_per_row)
images = [instance.reshape(size,size) for instance in instances]
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = mpl.cm.binary, **options)
plt.axis("off")
plt.figure(figsize=(7, 4))
plt.subplot(121)
plot_digits(X_train[::2100])
plt.title("Original", fontsize=16)
plt.subplot(122)
plot_digits(X_recovered[::2100])
plt.title("Compressed", fontsize=16)
save_fig("mnist_compression_plot")</pre>

#### 增量PCA (IPCA)
分批处理数据集
<pre class="EnlighterJSRAW" data-enlighter-language="null">from sklearn.decomposition import IncrementalPCA
n_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_train, n_batches):
print(".", end="") # not shown in the book
inc_pca.partial_fit(X_batch)
#np.array_split --> partial_fit
X_reduced = inc_pca.transform(X_train)</pre>
或者使用Numpy的**memmap**类,达到同样的效果
<pre class="EnlighterJSRAW" data-enlighter-language="null">filename = "my_mnist.data"
m, n = X_train.shape
X_mm = np.memmap(filename, dtype="float32", mode="readonly", shape=(m, n))
batch_size = m // n_batches
inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size)
inc_pca.fit(X_mm)
</pre>
#### 随机PCA
快速找到前d个主成分的近似值,当d<<n时,它比前面的算法要快得多
<pre class="EnlighterJSRAW" data-enlighter-language="null">rnd_pca = PCA(n_components=154, svd_solver="randomized", random_state=42)
X_reduced = rnd_pca.fit_transform(X_train)
</pre>
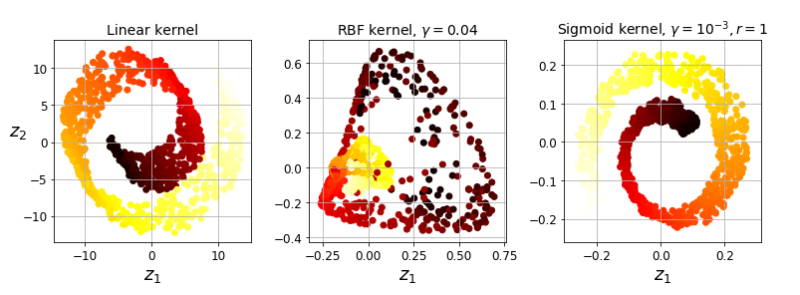
#### Kernel-PCA
<pre class="EnlighterJSRAW" data-enlighter-language="null">X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
from sklearn.decomposition import KernelPCA
lin_pca = KernelPCA(n_components = 2, kernel="linear", fit_inverse_transform=True)
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.0433, fit_inverse_transform=True)
sig_pca = KernelPCA(n_components = 2, kernel="sigmoid", gamma=0.001, coef0=1, fit_inverse_transform=True)
y = t > 6.9
plt.figure(figsize=(11, 4))
for subplot, pca, title in ((131, lin_pca, "Linear kernel"), (132, rbf_pca, "RBF kernel, $\gamma=0.04$"), (133, sig_pca, "Sigmoid kernel, $\gamma=10^{-3}, r=1$")):
X_reduced = pca.fit_transform(X)
if subplot == 132:
X_reduced_rbf = X_reduced
plt.subplot(subplot)
#plt.plot(X_reduced[y, 0], X_reduced[y, 1], "gs")
#plt.plot(X_reduced[~y, 0], X_reduced[~y, 1], "y^")
plt.title(title, fontsize=14)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
plt.xlabel("$z_1$", fontsize=18)
if subplot == 131:
plt.ylabel("$z_2$", fontsize=18, rotation=0)
plt.grid(True)
save_fig("kernel_pca_plot")
plt.show()</pre>
##### 选择核函数&调整超参数
<pre class="EnlighterJSRAW" data-enlighter-language="null">from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
# 先降至二维,然后用逻辑回归分类
clf = Pipeline([
("kpca", KernelPCA(n_components=2)),
("log_reg", LogisticRegression(solver="liblinear"))
])
# 寻找最优核、gamma值
param_grid = [{
"kpca__gamma": np.linspace(0.03, 0.05, 10),
"kpca__kernel": ["rbf", "sigmoid"]
}]
grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)
print(grid_search.best_params_)</pre>
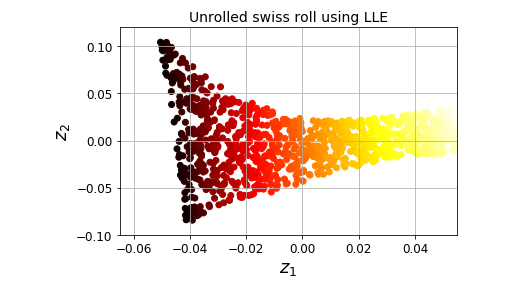
### 局部线性嵌入 Locally Linear Embedding
- 属于流形学习方法

<pre class="EnlighterJSRAW" data-enlighter-language="null">X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=41)
from sklearn.manifold import LocallyLinearEmbedding
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10, random_state=42)
X_reduced = lle.fit_transform(X)
# 可视化
plt.title("Unrolled swiss roll using LLE", fontsize=14)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
plt.xlabel("$z_1$", fontsize=18)
plt.ylabel("$z_2$", fontsize=18)
plt.axis([-0.065, 0.055, -0.1, 0.12])
plt.grid(True)
save_fig("lle_unrolling_plot")
plt.show()</pre>
### MDS 多维缩放
> 保持实例之间的距离,降低维度。
<pre class="EnlighterJSRAW" data-enlighter-language="null">from sklearn.manifold import MDS
mds = MDS(n_components=2, random_state=42)
X_reduced_mds = mds.fit_transform(X)</pre>
### Isomap 等度量映射
> 将每个实例和与其最近的邻居相连接,创建连接图形,保留实例间的测地距离(2个节点最短路径上的节点数),降低维度
<pre class="EnlighterJSRAW" data-enlighter-language="null">from sklearn.manifold import Isomap
isomap = Isomap(n_components=2)
X_reduced_isomap = isomap.fit_transform(X)</pre>
#### t-SNE(t-分布随机近邻嵌入)
> 令相似的实例靠近,不相似的实例远离。主要用于可视化。
<pre class="EnlighterJSRAW" data-enlighter-language="null">from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, random_state=42)
X_reduced_tsne = tsne.fit_transform(X)</pre>
#### LDA 线性判别
> 实际上是分类算法,它所学习到的决策边界可以用来定义投影数据的超平面。
<pre class="EnlighterJSRAW" data-enlighter-language="null">from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis(n_components=2)
X_mnist = mnist["data"]
y_mnist = mnist["target"]
lda.fit(X_mnist, y_mnist)
X_reduced_lda = lda.transform(X_mnist)</pre>
### 聚类
> 有时间再看。
[读书笔记]Hands-on ML 降维
